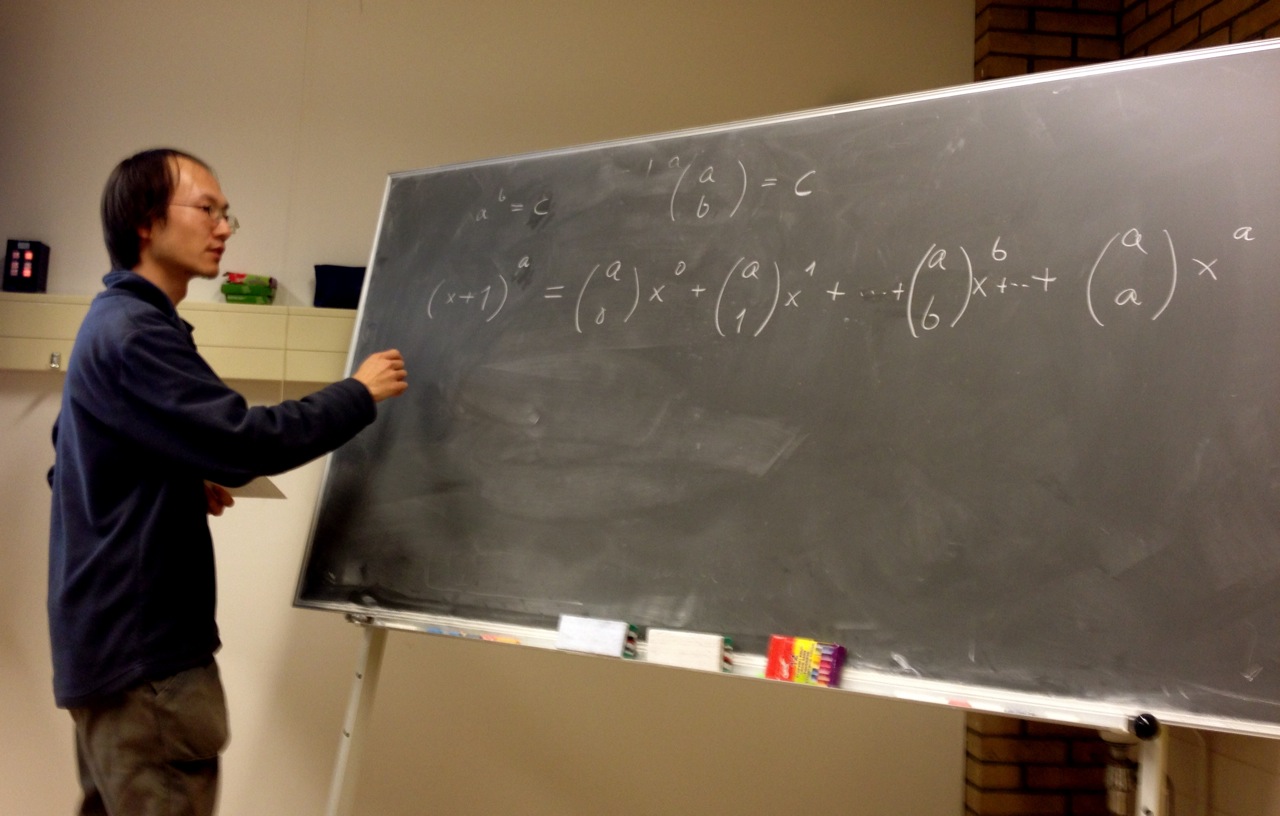Yuning Feng
(ILLC)
Delicacies without a recipe - Hilbert's Tenth Problem is unsolvable!
December 6th at 17:30, in ILLC Seminar Room (F1.15)
Diophantine equations are equations involving only integers, additions and multiplications (e.g. x=2y+1). Despite the elementary form, finding solutions for those equations can be difficult, sometimes impossible (e.g. Fermat's Last Theorem). In 1900, mathematician David Hilbert listed several important open mathematical problems, the tenth of which quested a testing procedure that could tell whether an arbitrary Diophantine equation has a solution. The problem was finally settled in the 1970s: there is no such a procedure! In this talk, we will take a look at the precise formulation of the problem and the overall idea of the proof.